Depois de fazermos a engenharia de dados, ajustes, seleção do modelo e obter alguma saída na forma de probabilidade ou classe a próxima etapa é descobrir quão eficaz é o modelo baseado em alguma métrica.

“Aquilo que não podemos medir, não podemos controlar.” Vicente Falconi

A métrica explica e compara o desempenho entre os diferentes modelos utilizados no algorítimo.

Um modelo ainda pode apresentar resultados satisfatórios quando avaliados por uma métrica, mas fornecer resultados reais ruins quando colocado em atividade. A escolha da métrica influencia o desempenho de aprendizado de máquina e como avaliamos a importância de diferentes características nos resultados.

Conforme documentação do Scikit Learning as métricas podem ser divididas em três grandes blocos: Classificação, Clustering(agrupamento) e Regressão.

Neste post irei abordar os métodos mais comuns utilizados em Regressão e Classificação. Caso deseje se aprofundar no assunto a documentação oficial é um ótimo ponto de partida.

Regressão

MAE: Mean Absolut Error

É a média da diferença do módulo entre o valor original e o valor de previsão obtido pelo modelo; Não fornece referência para a direção do erro; Influenciado por outliers; Atribui o mesmo peso para todas as diferenças.

No gráfico a baixo podemos obsevar o que são as diferenças entre a média linha e o valor pontos:

Amplitude: 0 ao + infinito.

Quanto menor o erro melhor o modelo.

A fórmula para cálculo é: \(Mean\ Absolut\ Error = \frac{1}{m} \sum_{i=1}^{n} \left\lvert y_i - \hat{y}_i \right\rvert\)

MSE: Mean Square Error

Utiliza a média do quadrado do módulo da diferença entre o valor original e o valor de previsão obtido pelo modelo; Como considera-se o quadrado da diferença penaliza maiores errros; Muito influenciável por outliers; Antes de utilizarmos essa métrica devemos eliminar os valores nulos e outliers do dataset;

A fórmula para cálculo é: \(Mean\ Squared\ Error = \frac{1}{N} \sum_{i=1}^{N} (y_{i} - \hat{y_{i}})^2\)

Amplitude: 0 ao +infinito Quanto menor o erro melhor o modelo.

RMSE: Root Mean Squarre Error

Calcula a raíz quadrada dos erros do modelo ao quadrado da diferença entreo o valor original a e o valor de previsão obtido pelo modelo; RMSE é a raíz do MSE; Como as métricas RMSE e MSE são elevadas ao quadrado, ambas são muito influenciadas por outliers;

A fórmula para cálculo é: \(Root\ Mean\ Squared\ Error =\sqrt{ \frac{1}{N} \sum_{i=1}^{N} (y_{i} - \hat{y_{i}})^2}\)

Normalmente RMSE é maior ou igual ao MSE.

Classificação

Como se avalia um modelo de classificação?

Seja trabalhando com classificação binária ou com diversas classes, as métricas relacionadas a modelos de classificação não podem ser os mesmos que usamos em modelos de regressão.

Accuracy ou Acurácia

Contabiliza a taxa de acertos; Mede o quão próximo o modelo está dos valores reais; Deve ser utilizada quando temos um dataset com dados balanceados;

Resumidamente podemos falar que acurácia é: \(= \frac{\text{Número de previsões corretas}}{\text{Número total de previsões}}\)

Ou podemos definir que é a média global de acertos ao classificar as classes.

Em relação as previsões podemos dividí-las em:

Tipos de erros:

• Verdadeiro positivo (true positive — TP): Por exemplo, quando o paciente tem tumor maligno e o modelo classifica como tendo tumor maligno.

• Falso positivo (false positive — FP): Por exemplo, quando o paciente não tem tumor maligno e o modelo classifica como tendo tumor maligno.

• Falso negativo (true negative — TN): Por exemplo, quando o paciente tem tumor maligno e o modelo classifica como não tendo tumor maligno.

• Verdadeiro negativo (false negative — FN): Por exemplo, quando o paciente não tem tumor maligno e o modelo classifica como não tendo tumor maligno.

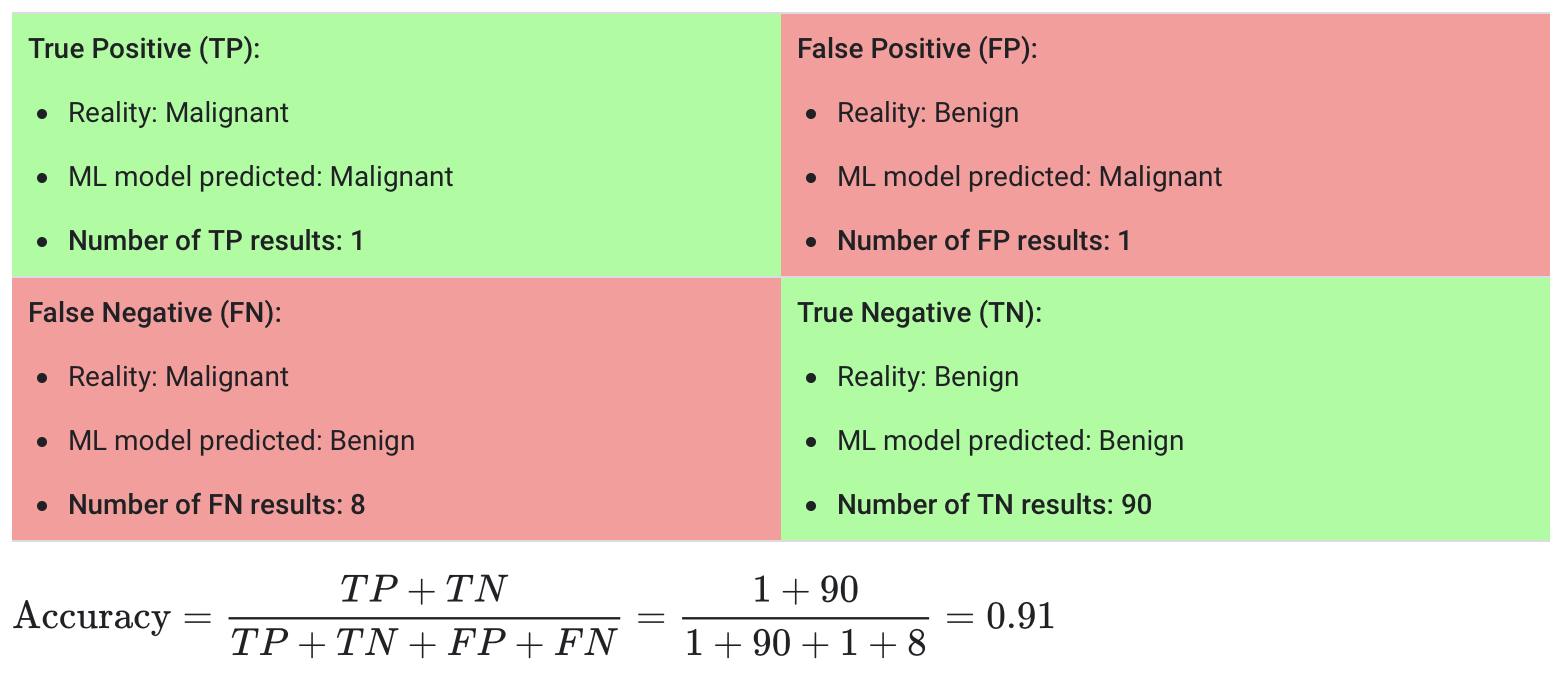
A fórmula para cálculo é: \(Acuracia = \frac{Number\ of\ correct\ predictions}{Total\ number\ of\ predictions\ made} = \frac{TP + TN}{TP + TN + FP + FN}\)

Sensibilidade: mostra a proporção dos classificados como positivos em relação ao total de positivos

[Sensibilidade = \frac{TP}{TP + FN}]

Especificidade: mostra proporção dos classificados como negativos em relação ao total de negativos

[Especificidade = \frac{TN}{TN+FP}]

Como nos foi apresentado a matriz acima podemos nos aprofundar um pouco mais nos conceitos:

Precisão

Número de exemplos classificados como pertencentes a uma classe que realmente são daquela classe, dividido pela soma destes números e o número de exemplos classificados nesta classe, ou seja, proporção previsões positivas corretas e todas as previsões positivas.

[= \frac{TP}{TP+FP}]

O valor máximo será 1.

Recall

Número de exemplos classificados como pertecentes a uma clase, que realmente são, dividido pelo total de exemplos que pertencem a essa classe. Relação entre previsões positivas corretas e todas as previsões positivas.

Recall = \(\frac{TP}{TP+FN}\)

F1-Score

É a média harmônica entre precisão e recall. Muito utilizado em datasets desbalanceados. O melhor resultado para o F1-Score é 1.

É calculado por: \(2* \frac{precision*recall}{precision+recall}\)

Matriz de Confusão

A matriz de confusão é uma matriz quadrada onde comparamos os valores verdadeiros de uma classificação com os valores de previsão de alguns modelos. Na diagonal principal dessa matriz quadrada estão os valores corretos e na matriz secundária os erros cometidos pelo modelo.

O algorítimo do Scikit Learn nos permite com um simples comando invocar as métricas aqui apresentadas em forma de sumário:

  #importando a biblioteca necessária
  from sklearn.metrics import classification_report

  #exemplo de valores
  y_true = [0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0]
  y_pred = [0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0]

  #evocando o report de classificação
  print(classification_report(y_true, y_pred))
  

Conclusão

Tão importante quanto definir um modelo é escolher a métrica correta para avaliá-lo!

O aprendizado de máquina oferece uma grande variedade de maneiras úteis de abordar problemas que, de outra forma, desafiam a solução manual. No entanto, muitas pesquisas atuais de ML sofrem de um distanciamento crescente desses problemas reais. Muitos pesquisadores retiram-se para seus estudos privados com uma cópia do conjunto de dados e trabalhar isoladamente para aperfeiçoar desempenho algorítmico. Publicação de resultados na comunidade de ML é o fim do processo. Sucesso geralmente não são comunicados de volta ao problema original configuração, ou não em uma forma que possa ser usada. No entanto, essas oportunidades de impacto real são generalizadas. Os mundos do direito, finanças, política, medicina, educação e muito mais podem se beneficiar de sistemas que podem analisar, adaptar e aceitar (ou pelo menos recomendar) uma ação.

Motivação

Data Science na Prática

O material aqui desenvolvido é parte da provocação feita no curso de Data Science na Prática onde fui desafiado a tentar explicar os passos e ferramentas aplicadas durante a evolução do material.

Todo o material a ser desenvolvido no curso será centralizado no meu portfolio de projetos.

Para saber mais sobre o curso acesse https://sigmoidal.ai

Fontes

• Documentação oficial: Scikit Leaning
• How to choose right metric from Kaggle: Link
• Notebook desenvolvido durante o curso: Colab
• Machine Learning that Matters: Paper